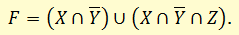Для каждой формулы алгебры высказываний можно указать равносильную ей формулу, содержащую из логических связок лишь отрицание, конъюнкцию и дизъюнкцию. Для этого нужно, используя равносильности теорем из прошлого параграфа, выразить все имеющиеся в формуле импликации и эквивалентности через отрицание, конъюнкцию и дизъюнкцию.
Так, для формулы (¬X∩(X→Y)) равносильной ей формулой, не содержащей логических связок и , будет, например, формула (¬X∩(¬X∪Y))∪Y. Выразить данную формулу через отрицание, конъюнкцию и дизъюнкцию возможно не одним способом, а многими. К примеру, рассматриваемая формула равносильна также следующим формулам, содержащим из логических связок лишь отрицание, конъюнкцию и дизъюнкцию:X∪Y, (X∪Y)∩(¬Y∪Y), (X∩¬Y)∪(X∩Y)∪(¬X∩Y) и др.
Конъюнктивным одночленом от переменных X1, X2,…, Xn называется конъюнкция этих переменных или их отрицаний. Здесь «или »употребляется в неисключающем смысле, т.е. в конъюнктивный одночлен может входить одновременно и переменная, и ее отрицание. Приведем несколько примеров конъюнктивных одночленов:
X1∩X2∩X3, X1∩¬(X2)∩X3∩X4, X1∩¬(X2)∩¬(X3)∩¬(X3)∩X4∩X5.
Дизъюнктивным одночленом от переменных X1, X2,…, Xn называется дизъюнкция этих переменных или их отрицаний, здесь союз «или» употребляется в неисключающем смысле.
Примеры дизъюнктивных одночленов:
¬(X1)∪X2∪X3, X1∪X2∪X3∪X4, X1∪X2∪¬(X3)∪¬(X1)∪X4∪X2.
Дизъюнктивной нормальной формой называется дизъюнкция конъюнктивных одночленов, т.е. выражение вида K1∪K2∪…∪Kr, где все Ki, i=1,2,…,r, являются конъюнктивными одночленами (не обязательно различными).
Аналогично, конъюнктивной нормальной формой называется конъюнкция дизъюнктивных одночленов D1∪D2∪…∪Dp, где все Dj, j=1,2,…,p, являются дизъюнктивными одночленами (не обязательно различными).
Также дизъюнктивной или конъюнктивной нормальной формой указанные выражения при r = 1 или p = 1.
Нормальную форму, представляющую формулу F (то есть равносильную F), будем называть просто нормальной формой этой формулы.
Понятно, что всякая формула обладает как дизъюнктивной, так и конъюнктивной нормальными формами. В самом деле, всякую формулу можно выразить через конъюнкцию, дизъюнкцию и отрицание. Используя законы де Моргана и свойство дистрибутивности конъюнкции относительно дизъюнкции, можем преобразовать равносильным образом полученное выражение к дизъюнкции конъюнктивных одночленов (к дизъюнктивной нормальной форме). Если же к исходному выражению применить свойство дистрибутивности дизъюнкции относительно конъюнкции, то его можно свести к конъюнкции дизъюнктивных одночленов (к конъюнктивной нормальной форме).
Очевидно, что у формулы F существует неограниченно много как дизъюнктивных, так и конъюнктивных нормальных форм. Одни из них более громоздкие и сложные, другие — более простые.
Алгоритм построения КНФ и ДНФ.
1) Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы:
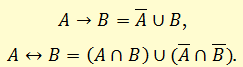
2) Заменить знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимися к отдельным переменным высказываниям на основании закона Де-Моргана:
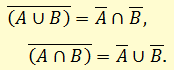
3) Избавиться от знаков двойного отрицания:
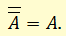
4) Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.
Пример построения КНФ.
Приведем к КНФ формулу

Преобразуем формулу F к формуле не содержащей импликацию:
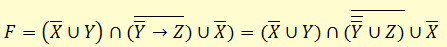
В полученной формуле перенесем отрицание к переменным и сократим двойные отрицания:
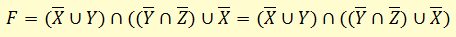
По закону дистрибутивности получим КНФ:
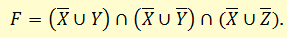
Пример построения ДНФ
Приведем к ДНФ формулу:
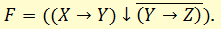
Выразим логические операции импликации и стрелку Пирса через конъюнкцию, дизъюнкцию и инверсию:
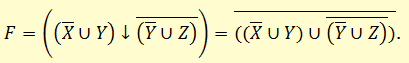
В полученной формуле перенесем отрицание к переменным и сократим двойные отрицания:
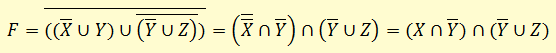
Используя закон дистрибутивности, приводим формулу к ДНФ: