Как и в любой науке, в логике главное — законы. Логических законов много, и в этом ее отличие от других наук. Однородные законы объединяются в логические системы, которые тоже обычно именуются логиками.
Правильное, или, как обычно говорят, логичное, мышление — это мышление по законам логики, по тем абстрактным схемам, которые фиксируются ими. Законы логики составляют тот невидимый каркас, на котором держится последовательное рассуждение и без которого оно превращается в хаотическую, бессвязную речь.
- Свойства констант.
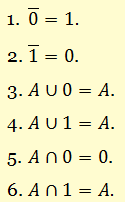
- Закон тождества.
Самый простой из всех логических законов — это, пожалуй, закон тождества. Он говорит: если утверждение истинно, то оно истинно, «если А, то А».
A=A.
Например, если Земля вращается, то она вращается и т.п.
- Закон двойного отрицания.
Законы двойного отрицания позволяют снимать и вводить такое отрицание.
Их можно выразить так: если неверно, что не-А, то А; если А, то неверно, что не-А.
Например: «Если неверно, что Аристотель не знал закона двойного отрицания, то Аристотель знал этот закон», и наоборот.
Закон двойного отрицания был известен ещё в античности. В частности, древнегреческие философы Зенон Элейский и Горгий излагали его следующим образом: если из отрицания какого-либо высказывания следует противоречие, то имеет место двойное отрицание исходного высказывания, то есть оно само.
В символической форме закон записывается так:
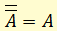
если неверно, что не-А, то верно А.
Другой закон логики, говорящий о возможности не снимать, а вводить два отрицания, принято называть обратным законом двойного отрицания: утверждение влечёт своё двойное отрицание.
Например: «Если Шекспир писал сонеты, то неверно, что он не писал сонеты».
Символически:
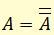
если А, то неверно что не—А.
Объединение этих законов даёт так называемый полный закон двойного отрицания:
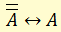
неверно, что не-А, если и только если верно А.
- Закон противоречия.
Из всего множества логических законов, самым популярным является закон противоречия. Он был открыт одним из первых и сразу же объявлен наиболее важным принципом не только человеческого мышления, но и самого бытия.
Закон противоречия говорит о противоречащих друг другу высказываниях, т. е. о таких высказываниях, одно из которых является отрицанием другого.
Например: «Луна — спутник Земли» и «Луна не является спутником Земли», «Трава — зеленая» и «Неверно, что трава зеленая» и т.п.
Другими словами, в одном из противоречащих высказываний что-то утверждается, в другом — это же самое отрицается.
Идея, выражаемая законом противоречия: высказывание и его отрицание не могут быть вместе истинными.
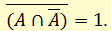
Например, неверно, что трава зеленая и не зеленая, что Луна спутник Земли и не спутник Земли и т.д.
Закон противоречия говорит о противоречащих высказываниях — отсюда его название. Но он отрицает противоречие, объявляет его ошибкой и тем самым требует непротиворечивости — отсюда другое распространенное имя — закон непротиворечия.
- Закон исключенного третьего.
Закон исключительного третьего, как и закон противоречия, устанавливает связь между противоречащими друг другу высказываниями.
Идея, выражаемая им: из двух противоречащих высказываний одно является истинным.
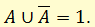
Конкретными приложениями этого закона являются, к примеру, высказывания: «Аристотель умер в 322 г. до н.э. или он не умер в этом году», «Личинки мух имеют голову или не имеют ее».
Истинность отрицания равнозначна ложности утверждения. В силу этого закон исключенного третьего можно передать и так: каждое высказывание является истинным или ложным.
- Закон рефлексивности (идемпотентности).
Закон идемпотентности - это закон математической логики, по которому из логики исключаются коэффициенты и показатели степеней. В логике присутствуют аналоги известных алгебраических законов:
а * а = a2; а + а = 2а,
но вычисляются они по своим правилам.
Так логическое умножение двух высказываний А есть A:
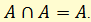
Читается так «А и А равносильно А».
Логическое сложение двух высказываний А, равносильно А
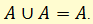
Читается: «А или А равносильно А», «А или А есть тоже самое, что А».
- Закон коммутативности.
Законами коммутативности называют логические законы, позволяющие менять местами высказывания, связанные «и» и «или». Эти законы аналогичны алгебраическим законам коммутативности для умножения, сложения и др., по которым результат умножения не зависит от порядка множителей, сложения — от порядка слагаемых и т.д.
Символически законы коммутативности для конъюнкции и дизъюнкции записываются так:
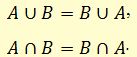
Примеры: «Завтра будет дождь или будет снег, если и только если завтра будет снег или завтра будет дождь», «Волга — самая длинная река в Европе и Волга впадает в Каспийское море в том и только том случае, если Волга впадает в Каспийское море и Волга является самой длинной рекой в Европе»».
- Закон ассоциативности.
Законами ассоциативности называются логические законы, позволяющие по-разному группировать высказывания, соединяемые с помощью «и», «или» и др.
Операции сложения и умножения чисел в математике ассоциативны:
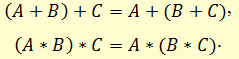
Ассоциативностью обладают также логическое сложение (дизъюнкция) и логическое умножение (конъюнкция). Символически соответствующие законы представляются так:
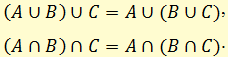
В силу законов ассоциативности в формулах, представляющих конъюнкцию более чем двух высказываний или их дизъюнкцию, можно опускать скобки.
- Закон дистрибутивности.
Закон дистрибутивности определяет правила раскрытия скобок в процедурах произведения множителя на сумму слагаемых. В математической логике закон определяет правила корректного проведения операций конъюнкции над членами дизъюнкции и выражается следующей формулой:
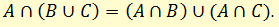
Что означает А и (В или С) есть тоже самое, что А и В или А и С.
В математической логике имеет место ещё второй закон дистрибутивности, выражающийся формулой:
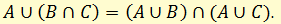
Что означает А или (В и С) есть тоже самое, что А или В и А или С.
- Закон поглощения.
Закон поглощения – это закон математической логики, согласно которому верны следующие равенства:
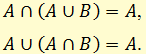
- Закон склеивания.
Логическая операция, в процессе которой два члена формулы, имеющие одинаковую часть, заменяются одним членом, как бы склеиваются, носит название закон склеивания.
Пусть имеется сложное высказывание
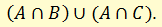
Анализируя это выражение, видим, что у двух членов конъюнкции имеется одинаковая часть высказывания - А. Тогда это высказывание можно упростить так:
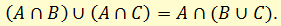
- Законы де Моргана.
Именем английского логика XIX в. А. Де Моргана называются логические законы, связывающие с помощью отрицания высказывания, образованные с помощью союзов «и» и «или».
Один из этих законов можно выразить так: отрицание высказывания «А и В» эквивалентно высказыванию «не-А или не-В».
Например: «Неверно, что завтра будет холодно и завтра будет дождливо, если и только если завтра не будет холодно или завтра не будет дождливо».
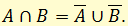
Другой закон: неверно, что А и В, если и только если неверно А и неверно В.
Например: «Неверно, что ученик знает арифметику или знает геометрию, если и только если он не знает ни арифметики, ни геометрии».
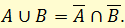
- Закон контрапозиции.
«Закон контрапозиции» — это общее название для ряда логических законов, позволяющих с помощью отрицания менять местами основание и следствие условного высказывания.
Один из этих законов, называемый иногда законом простой контрапозиции, звучит так:
если первое влечет второе, то отрицание второго влечет отрицание первого.
Например: «Если верно, что число, делящееся на шесть, делится на три, то верно, что число, не делящееся на три, не делится на шесть».
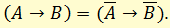
Еще два закона конрапозиции: если дело обстоит так, что если А, то не-В, то если В, то не-А; например: «Если квадрат не является треугольником, то треугольник не квадрат»
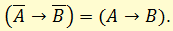
если верно, что если не-А, то В, то если не-В, то А; например: «Если не являющееся очевидным сомнительно, то не являющееся сомнительным очевидно»
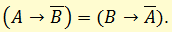
- Закон Клавия
Закон Клавия характеризует связь импликации и отрицания. Он читается так: если из отрицания некоторого высказывания вытекает само это высказывание, то оно является истинным. Или, короче: высказывание, вытекающее из своего собственного отрицания, истинно.
Например, если условием того, чтобы машина не работала, является её работа, то машина работает.
Закон назван именем Клавия — учёного-иезуита, жившего в XVI в., одного из изобретателей григорианского календаря. Клавий первым обратил внимание на этот закон в своём комментарии к «Геометрии» Евклида. Одну из своих теорем Евклид доказал, выведя из её допущения, что она является ложной.
Символически закон Клавия представляется формулой:
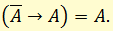
Из закона Клавия вытекает следующий совет, касающийся доказательства: если хочешь доказать А, выводи А из допущения, что верным является не-А.
Например, нужно доказать утверждение «У трапеции четыре стороны». Отрицание этого утверждения: «Неверно, что у трапеции четыре стороны». Если из этого отрицания удаётся вывести само утверждение, это будет означать, что оно истинно.
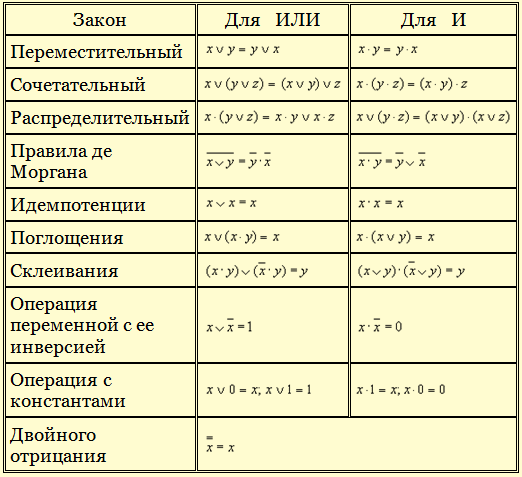
Основные положения:
Контрольные вопросы и задания:
1. В чем суть закона ассоциативности?
2. Приведите доказательства законов де Моргана?
3.

Литература:
- Сборник упражнений по логике. Под ред. Клевчеки С.
- Булатов М.А. Логические категории и понятия.
- Ивлев Ю.В. Логика.
- Угринович Н.Д. Информатика и информационные технологии. Учебник для 10–11 классов.




