В15 Решить систему уравнений с логическими переменными.
Пример:
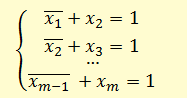
Сколько различных решений имеет система логических уравнений?
Решение (способ 1, бинарное дерево):
Приведенная система уравнений равносильна уравнению:
(x1 → x2)*( x2 → x3)*…*( xm-1 → xm) = 1.
Предположим, что x1 – истинно, тогда из первого уравнения получаем, что x2 также истинно. Далее из второго уравнения получаем, что x3 истинно, и т.д. до xm = 1. Значит набор (1; 1; …; 1) из m единиц является решением системы.
Пусть теперь x1 – ложно, тогда из первого уравнения следует, что x2 может быть как истинным, так и ложным, то есть может принимать значения как 0, так и 1.
В случае, если x2 истинно получаем, что остальные переменные также истинны, то есть набор (0; 1; …; 1) является решением системы. В случае, когда x2 – ложно получаем, что для x3 есть две возможности, 0 и 1, и так далее. Продолжая до последней переменной, получаем, что решениями уравнения являются следующие наборы переменных (m+1 решение, в каждом решении по m значений переменных):
(1; 1; 1; …; 1)
(0; 1; 1; …; 1)
(0; 0; 1; …; 1)
…
(0; 0; 0; …; 0)
Такой подход хорошо иллюстрируется с помощью построения бинарного дерева. Получив единицу, все остальные значения переменных также становятся единицами, получив же ноль, возможны два варианта 0 и 1. Для одного уравнения дерево состоит из двух уровней, для двух уравнений добавляется одна переменная и соответственно один уровень дерева. Количество возможных решений – количество различных ветвей построенного дерева. Легко заметить, что оно равно m+1.
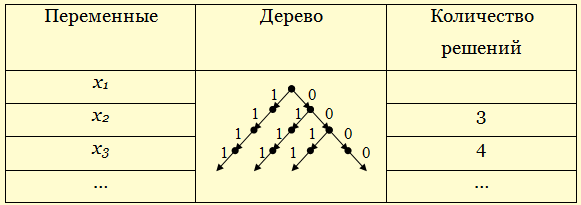
Решение (способ 2, построение таблиц истинности):
В случае трудностей в рассуждениях и построении дерева решений можно искать решение с использованием таблиц истинности, для одного – двух уравнений.
Перепишем с![]() истему уравнений в виде:
истему уравнений в виде:
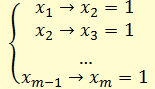
И составим таблицу истинности для одного уравнения:
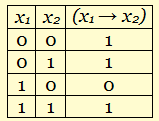
Составим таблицу истинности для двух уравнений:
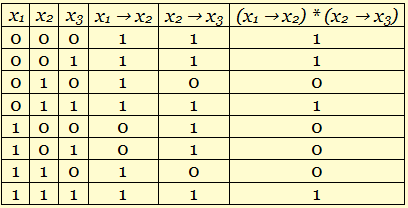
Далее можно увидеть, что одно уравнение истинно в следующих трех случаях: (0; 0), (0; 1), (1; 1).
Система двух уравнений истина в четырех случаях (0; 0; 0), (0; 0; 1), (0; 1; 1), (1; 1; 1). При этом сразу видно, что существует решение, состоящее из одних нулей и еще m решений, в которых добавляется по одной единице, начиная с последней позиции до заполнения всех возможных мест. Можно предположить, что общее решение будет иметь такой же вид. Хотя это, конечно, не решение, но ответ таким образом угадать можно. Для того, чтобы такой подход стал решением, требуется доказательство, что предположение верно.
Пример:
Сколько различных решений имеет система логических уравнений:
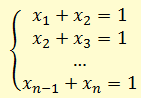
Решение (способ 3, числа Фибоначчи):
Решая систему, любым из вышеописанных методов, получим 5 различных решений: (0; 1; 0), (0; 1; 1), (1; 0; 1), (1; 1; 0), (1; 1; 1). Для системы из трех уравнений имеем 8 решений – (0; 1; 0; 1), (0; 1; 1; 0), (0; 1; 1; 1), (1; 0; 1; 0), (1; 0; 1; 1), (1; 1; 0; 1), (1; 1; 1; 0), (1; 1; 1; 1).
Проанализировав данную систему логических уравнений, можно сделать вывод: если первая переменная любого уравнения принимает значение 0, то вторая переменная этого же уравнения обязательно примет значение 1, в противном случае, произвольное значение 1 или 0.
Обозначим Nk – общее количество решений системы k уравнений, N_k^0, N_k^1 – количество решений этой системы, последняя переменная которых соответственно равна 0 или 1. Понятно, что N_1^0 = 1, N_1^1 = 2.
В общем виде общее количество решений системы логических уравнений запишется:
Nk = N_k^1 + N_k^0.
Для представленной системы, получаем такое рекуррентное соотношение, с начальными условиями N1 = 3, N2 = 5. Такому соотношению соответствуют числа Фибоначчи, то есть элементам числовой последовательности 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, …, в которой каждое последующее число равно сумме двух предыдущих чисел.
Fn= F(n-2)+F(n-1).
Сравнив начальные значения с последовательностью Фибоначчи, получаем, что количество различных решений равно (n+2)-му члену последовательности Фибоначчи Fn+2.
При n=10 получаем – F12 = 144, при n= 7, F9 = 34.




