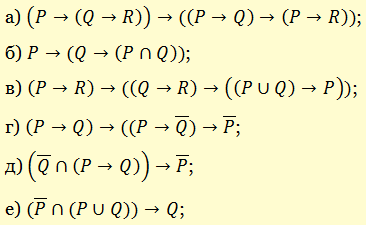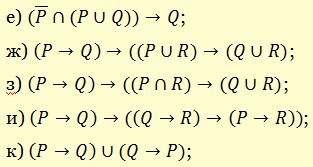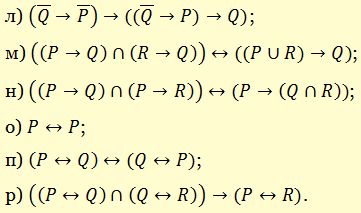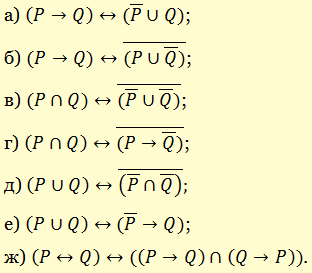В обычном языке слово «тавтология» означает повторение того, что уже было сказано: «Жизнь есть жизнь» или «Не повезет, так не повезет». Тавтологии бессодержательны и пусты, они не несут никакой информации. От них стремятся избавиться как от ненужного балласта, загромождающего речь и затрудняющего общение.
С легкой руки Л. Витгенштейна слово «тавтология» стало широко использоваться для характеристики законов логики. Став логическим термином, оно получило строгие определения применительно к отдельным разделам логики. В общем случае логическая тавтология — это выражение, остающееся истинным независимо от того, о какой области объектов идет речь, или «всегда истинное выражение».
Все законы логики являются логическими тавтологиями. Если в формуле, представляющей закон, заменить переменные любыми постоянными выражениями соответствующей категории, эта формула превратится в истинное высказывание.
Термин "тавтология" имеет греческое происхождение, составлен из двух слов ταντοζ (то же самое) и λογοζ (слово) и означает повторение одного и того же определения, суждения иными, близкими по смыслу словами. В тавтологиях, относящихся к математической логике, заключительной логической связкой является эквивалентность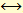 
. Например, тавтология
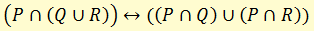
Совершенно аналогично в этом смысле арифметическое тождество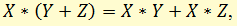
которое отражает ту же внутреннюю сущность посредством разных слов. И каждое из этих двух выражений является объективным законом, действующим каждый в своей сфере: первый — в сфере мыслительных процессов, второй — в сфере чисел. Каждый из этих законов несет объективную информацию об определенной части окружающего нас мира.
Приведем некоторые основные тавтологии, выражающие свойства логических операций, а также тавтологии, на которых основаны некоторые схемы математических доказательств.
а) закон исключенного третьего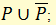 
б) закон отрицания противоречия
в) закон двойного отрицания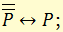 
г) закон тождества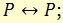 
д) закон контрапозиции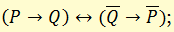 
е) закон силлогизма (правило цепного заключения)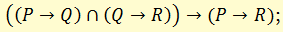 
ж) закон противоположности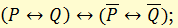 
з) правило добавления антецедента («истина из чего угодно»)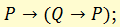 
и) правило «из ложного что угодно»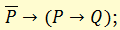 
к) правило «модус поненс» (лат. modus ponens)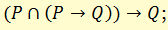 
л) правило «модус толленс» (лат. modus tollens)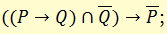 
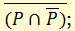
м) правило перестановки посылок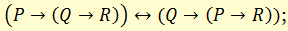 
н) правило объединения (и разъединения) посылок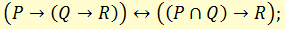 
о) правило разбора случаев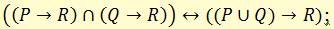 
п) правило приведения к абсурду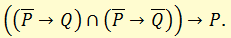 
Отметим, что непосредственно из определений логических операций вытекает тождественная истинность формул а), б), в), г); для формулы д) доказательство имеется. Установим тождественную истинность формул л) и н).
л) Изучая тавтологии, важно уяснить, что имеется простой и надежный алгоритм (общий метод), позволяющий для любой формулы логики высказываний дать ответ на вопрос, является она тавтологией логики высказываний или нет — этот алгоритм состоит в построении ее таблицы истинности. Составим таблицу истинности для правила «модус толленс»:
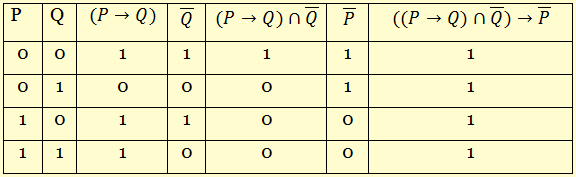
Последний столбец таблицы, состоящий из значений истинности данной формулы, содержит лишь единицы. Это означает, что данная формула — тавтология.
н) Доказательство тождественной истинности формул с помощью составления их таблиц истинности проходит автоматически. Приведем следующее доказательство, рассуждая о тех значениях, которые формула может принимать.
Покажем, что левая часть данной эквивалентности обращается в ложное высказывание тогда и только тогда, когда в ложное высказывание обращается формула, стоящая в правой части эквивалентности.
Действительно, формула P→(Q→R) превращается в ложное высказывание, если и только если P = 1, Q→R = 0. В свою очередь Q→R = 0, тогда и только тогда, когда Q = 1 и R = 0. Итак, P→(Q→R) = 0 в том и только в том случае, когда P = 1, Q = 1, R = 0. С другой стороны, формула (P∩Q)→R обращается в ложное высказывание, если и только если (P∩Q) = 1 и R = 0. В свою очередь, (P∩Q) = 1 тогда и только тогда, когда P = 1 и Q = 1. Итак, (P∩Q)→R = 0 в том и только в том случае, когда P = 1, Q = 1 и R = 0. Доказанное означает, что правая и левая части эквивалентности одновременно превращаются либо в истинные высказывания, либо в ложные. Следовательно, по определению эквивалентности вся формула всегда превращается в истинное высказывание, т.е. является тавтологией.
а) законы идемпотентности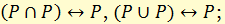 
б) законы упрощения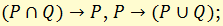 
в) законы коммутативности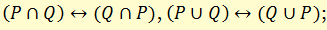 
г) законы ассоциативности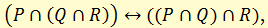 
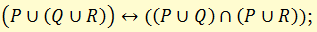
д) законы дистрибутивности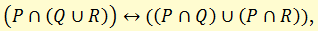 
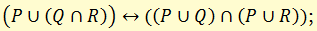
е) законы поглощения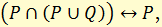 
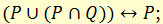
ж) законы де Моргана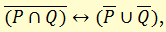 
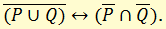
Следующие формулы алгебры высказываний являются тавтологиями:
