информатика и логика - Лекция 12. Методы решения логических задач.

3. Решение истинностных задач

Данный тип задач можно решать тремя методами: методом рассуждений, табличным методом и с помощью логических выражений, с помощью построения таблиц истинности и приведения задачи к системе логических уравнений.

Пример:

Перед началом Турнира «Четырех» болельщики высказали следующие предположения по поводу своих кумиров:

А) Макс победит, Билл – второй;

В) Билл – третий, Ник – первый;

С) Макс – последний, а первый – Джон.

Когда соревнования закончились, оказалось, что каждый из болельщиков был прав только в одном из своих прогнозов. Какое место на турнире заняли Джон, Ник, Билл, Макс?

Решение (способ 1, метод рассуждений):

1) Есть «точная» информация, которая не подвергается сомнению: каждый из болельщиков оказался прав в одном прогнозе.

2) Запишем высказывания болельщиков:

1. Макс победит, Билл – второй;
2. Билл – третий, Ник – первый;
3. Макс – последний, а первый – Джон.

3) Известно, что каждый из болельщиков только в одном из прогнозов был прав (то есть, из двух высказываний одно истинно, а другое – ложно).

4) Пусть первый болельщик угадал, что Макс победит, тогда третий болельщик ошибся в двух предположениях, а это не соответствует «точной» информации.

5) Пусть первый болельщик угадал, что Билл занял второе место, тогда второй болельщик предсказал первое место Нику, следовательно, по предположению третьего, Макс занял последнее место, а Джон – оставшееся третье место.

Отсюда имеем: Ник – первое, Билл – второе, Джон – третье и Макс – четвертое место.

Решение (способ 2, табличный метод):

Основной прием, который используется при решении текстовых логических задач, заключается в построении таблиц. Таблицы не только позволяют наглядно представить условие задачи или ее ответ, но в значительной степени помогают делать правильные логические выводы в ходе решения задачи.

1) Запишем высказывания трех болельщиков в форме таблицы (заголовок строки обозначает место в турнирной таблице):

2) Считая, что два человека не могут оказаться на одном месте, начнем «раскручивать» эту таблицу с той строчки, где больше всего информации (в данном случае – с первой).

3) Предположим, что Макс действительно занял первое место, как и сказал «A»; в этом случае:

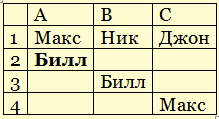
«C» ошибся, поставив на первое место Джона;
учитывая, что каждый один раз угадал, а второй ошибся, получается, что «C» угадал, что Макс будет на четвертом месте;
но мы предположили, что Макс – на первом месте (а не на четвертом), следовательно, получили противоречие; это значит, что Макс все-таки не на первом месте
таким образом, в первом прогнозе «А» ошибся, это значит, что во втором он угадал, и Билл действительно занял второе место:

так как Билл – второй, он не может быть на третьем месте, поэтому из прогноза «Б» следует, что Ник – первый:

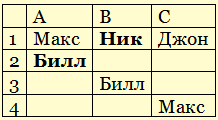
если Ник на первом месте, там не может быть Джон, поэтому из ответов «С» (среди которых должен быть один верный, и один неверный), сразу находим, что Макс занял четвертое место:

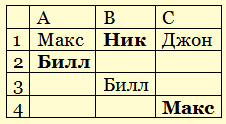
4) осталось только определиться с Джоном – ему досталось единственное «свободное» третье место; окончательный список победителей:

1. Ник

2. Билл

3. Джон

4. Макс.

Пример:

В школе-новостройке в каждой из двух аудиторий может находится либо кабинет информатики, либо кабинет физики. На дверях аудиторий повесили шутливые таблички. На первой повесили табличку «По крайней мере, в одном из этих аудиторий размещается кабинет информатики», а на второй аудитории – табличку с надписью «Кабинет физики находится в другой аудитории». Проверяющему, который пришел в школу, известно только, что надписи на табличках либо обе истины, либо обе ложны. Помогите проверяющему найти кабинет информатики.

Решение (способ 3, логические выражения):

Переведем условие задачи на язык логики высказываний. Так как в каждой из аудиторий может находиться кабинет информатики, то пусть:

А = «В первой аудитории находится кабинет информатики»;

В = «Во второй аудитории находится кабинет информатики».

Отрицания этих высказываний:

¬А =«В первой аудитории находится кабинет физики»;

¬В = «Во второй аудитории находится кабинет физики».

Х = А ˅ В.

Высказывание на второй двери:

Утверждение о том, что надписи на табличках либо одновременно истинные, либо одновременно ложные в соответствии с законом исключенного третьего запишется следующим образом:

Подставим вместо X и Y соответствующие формулы:

Упростим сначала первое слагаемое. В соответствии с законом дистрибутивности умножения относительно сложения:

В соответствии закона непротиворечия:

Далее упростим второе слагаемое. В соответствии с первым законом де Моргана и законом двойного отрицания:

В соответствии с законом непротиворечия:

В результате получаем:

Построим таблицу истинности для полученного выражения:

Проанализировав данные таблицы истинности имеем, что в первой аудитории находится кабинет физики, а во второй – кабинет информатики.

Пример:

Следующие два высказывания истинны:

(1). Неверно, что если корабль A вышел в море, то корабль C — нет.

(2). В море вышел корабль B или корабль C, но не оба вместе.

Определить, какие корабли вышли в море.

Решение (способ 4, система логических уравнений):

Обозначим буквами высказывания:

A — «корабль A вышел в море»,

B — «корабль B вышел в море»,

C — «корабль C вышел в море».

Высказывание «если корабль A вышел в море, то корабль C — нет» можно записать в виде:

По условию (1), это высказывание неверно, таким образом, имеем:

Кроме того, из (2) получаем:

Таким образом, решение задачи сводится к решению системы логических уравнений:

Нужно найти тройку логических значений A, B и C, при которых оба уравнения превращаются в истинные равенства. Рассмотрим несколько способов решения этой системы.

Способ 1. Сведение к одному уравнению.

Преобразуем уравнения так, чтобы правые части были равны 1 (истинному значению). Для этого применим инверсию (операцию «НЕ») к первому уравнению:

Теперь представляем импликацию и «исключающее ИЛИ» через базовые операции «И», «ИЛИ», «НЕ»:

Объединить оба уравнения с помощью операции «И» в одно уравнение, равносильное исходной системе:

Раскрываем инверсию в первой скобке по закону де Моргана и совершаем необходимые преобразования, после чего получим:

Последнее уравнение, равносильное исходной системе, имеет единственное решение: A = 1, B = 0 и C = 1. Таким образом, в море вышли корабли А и C.

Способ 2. Таблица истинности.

Построим таблицу истинности для системы с тремя переменными:

Полужирным выделена строка, для которой выполняются условия задачи. Таким образом, A = 1, B = 0 и C = 1 , это значит, что в море вышли корабли А и C. Недостаток этого метода — трудоемкость при большом количестве переменных.

Способ 3. Декомпозиция.

Идея состоит в том, чтобы зафиксировать значение одной из переменных (положить ее равной 0 или 1) и за счет этого упростить уравнения. Затем можно зафиксировать значение второй переменной и т.д.

При A = 0 получаем:

На основе определения импликации можно сделать вывод о том, что первое уравнение (и, следовательно, вся система) при A = 0 решений не имеет. Рассмотрим второй случай, при A = 1:

Из первого уравнения в следует, что или С = 1, а из второго — B = 0. Таким образом, существует единственное решение системы: A = 1, B = 0 и C = 1; это значит, что в море вышли корабли А и C.

Способ 4. Последовательное решение уравнений.

В некоторых случаях можно решать уравнения последовательно, на каждом шаге добавляя по одной переменной в рассматриваемый набор. Для данного способа удобнее вводить переменные в алфавитном порядке, для этого поменяем местами уравнения в системе:

Мы видим, что первое уравнение зависит только от A и B, а в третьем подключается переменная C. Будем строить дерево решений. Переменная А может принимать 2 значения:

Из первого уравнения

поэтому при A = 0 получаем единственный вариант B = 1, а при A = 1 имеем B = 0. Итак, первое уравнение имеет два решения относительно переменных A и B:

Теперь «подключаем» второе уравнение

из которого нужно определить допустимые значения C для каждого варианта. При A = 0 импликация не может быть ложна, то есть первая ветка дерева не дает ни одного решения системы двух уравнений. При A = 1 получаем единственное решение, для которого C = 1:

Таким образом, существует единственное решение системы: A = 1, B = 0 и C = 1. Это значит, что в море вышли корабли А и C.

Назад Решать задачи

Форма входа

Поиск

Календарь

Статистика